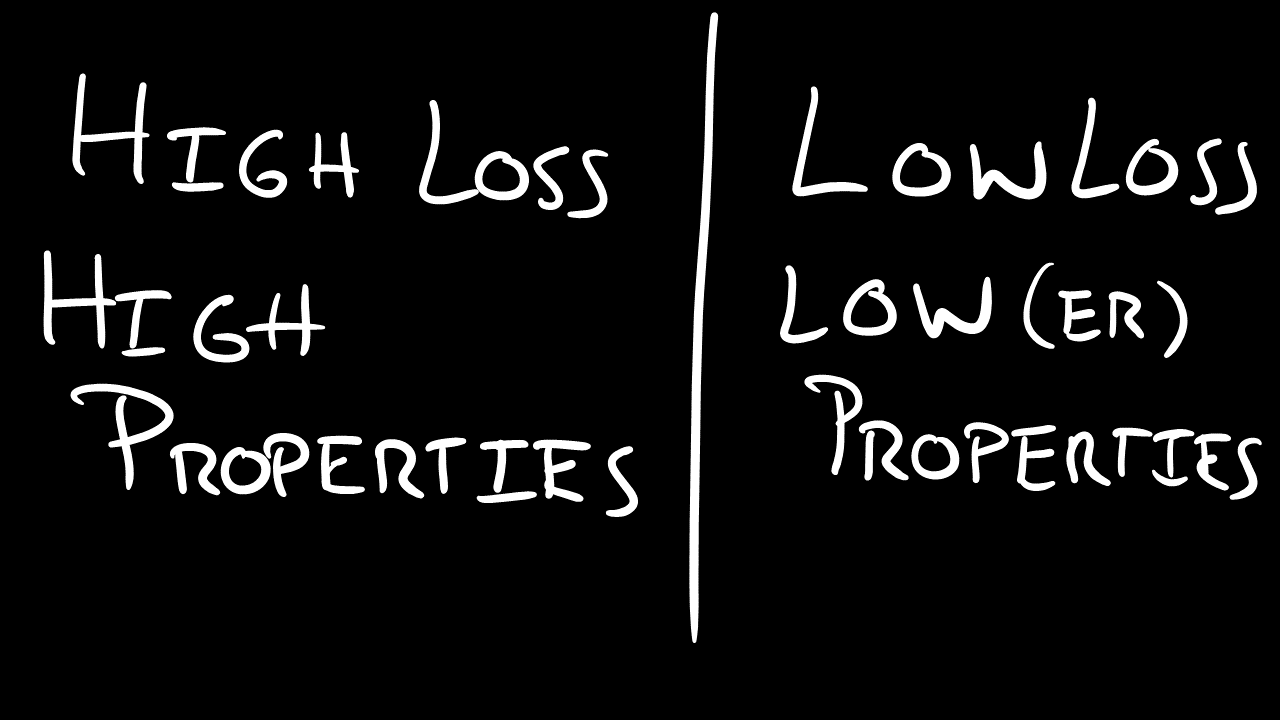The link between losses and piezo properties

Due to material microstructure phenomenon, larger piezoelectric constants in terms of the piezoelectric charge constant and the permittivity will always be accompanied with larger losses. This is because the phenomenon (domain wall motion) responsible for increasing the properties also increases irreversible energy transfer appearing as losses.

The apparent property, the real property, and the "loss" property

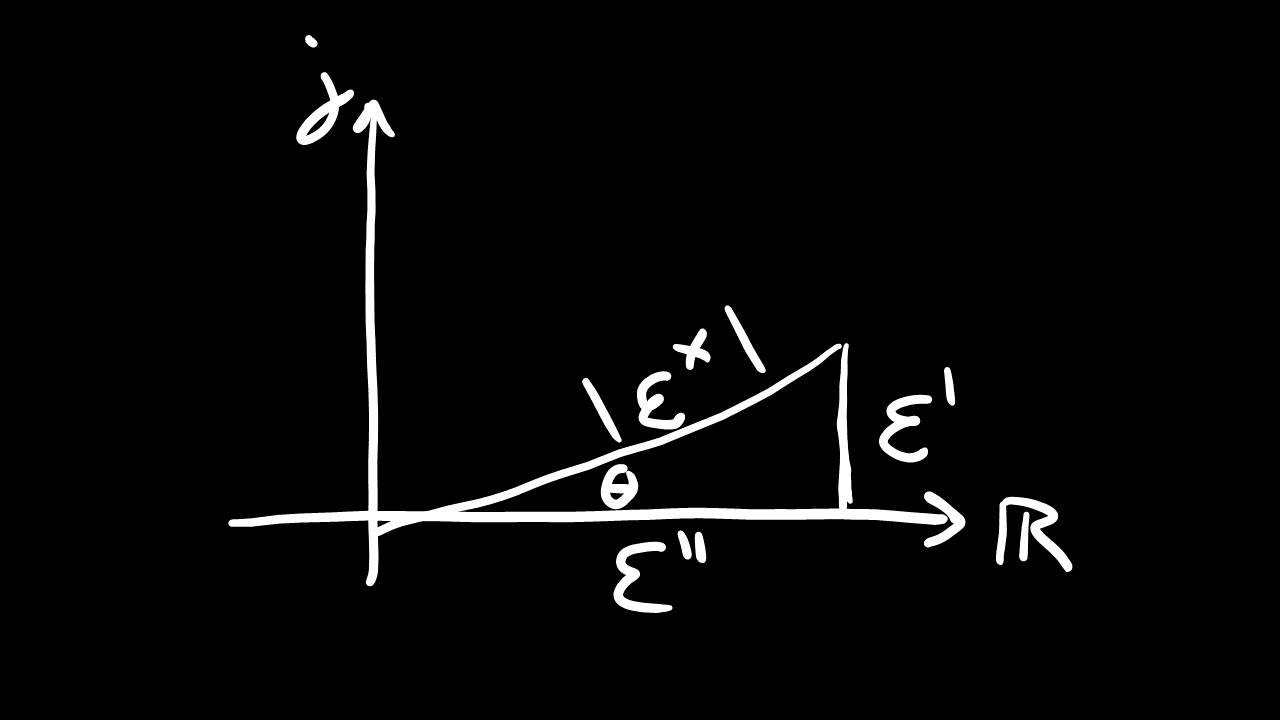
Describing losses opens up a new can of worms for the mathematical description of losses. The apparent material property is actually a complex number. So, for example, if you charged up a piezo, you will not be able to recover all of the energy by charging back down. The difference, also known as hysteresis losses, will represent the lost energy and the recoverable energy is known as the true stored energy. 

So, in order to describe the apparent property, we can either use complex number notation where the stored energy property is the "real" component and the loss property is the "imaginary" component. However, typically, we take the magnitude of the complex value ( like this: sqrt(A^2+B^2)) and the phase angle between the real and imaginary value to find the "loss factor". It's a fact of nature (and math) that the loss factor also is the exact same thing as the phase angle between input and output values (eg voltage and charge). Typically, because the loss factor is small, the apparent property is very close to the real property.



An example to answer the question

So, what if we had two material with the same apparent material properties (piezo charge coefficient, compliance, and permittivity) but one had 10x the losses of the other, what would be the difference in the voltage generated in:

1. Static or low frequency
2. Resonance

Static Case

In the static condition, the difference between the two material is very small. Even if losses of tan delta =  2% were given to the high loss material, the apparent material properties would change very little.

However, there would be a difference. A more lossy material would appear slightly stiffer than a low loss material, assuming their "real" properties were the same. Therefore, the strain would be lower for the high loss material and thus the voltage would be slightly lower.

All this being said, losses play a small role in static operation of devices, so typically the benefits of high piezo constants far outweigh the disadvantage of high losses.



Resonance Case

This one is gonna be obvious. The resonance strain is highly affected by the loss factors. This is because low losses give a direct amplification to energy stored in the oscillator. So, the material with low losses is going to trump the high loss material with force excitation at the resonance frequency.